The Day-Stout-Warren (DSW) Algorithm
The Day-Stout-Warren algorithm balances a binary search tree. This balancing produces a tree that not only has a minimum height, but also also forces all the nodes on the bottommost level to be filled from left to right. The running time is O(n), where 'n' is the number of nodes in tree.
|
Unbalanced Tree
Unbalanced tree. Height is 6.
|
Balanced Tree
Balanced tree. Height is 4.
|
DSW Balanced Tree
Balanced tree where bottommost nodes are all to the left. Height is 4.
|
Refresher On Binary Search Trees
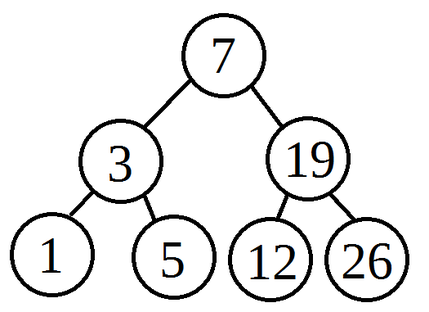
Binary Search Trees
|
The DSW algorithm is very specific to binary trees.
As a reminder, a binary tree is a tree like data structure holding "nodes." A node is a data structure itself that holds three values, the actual data in the node itself, a pointer to a left child (another node), and a pointer to a right child (another node). What makes a binary search tree work is that all children to the left of a node have values that are smaller than the value in the parent node, and all right children have values greater than the parent node's value. A binary tree is useful because the structure makes searching for values quick. Specifically, with a good binary tree we can find values in log(n) time. There are three special operations we can do to a binary tree. 1. Insertion - this one is easy, we can add a node to the tree. 2. Deletion - this can get complicated because of children nodes, but deleting nodes isn't relevant for the DSW algorithm. 3. Rotations - VERY important for the DSW algorithm. Let's go into detail. |
A node is just a structure that holds information.
A binary search tree is drawn like this.
|
Rotations
Rotations act on specific nodes. A rotation swaps the positions of nodes. Simple, right? Well, just saying it doesn't mean much, but the pictures will make it easy.
Rotations act on specific nodes. A rotation swaps the positions of nodes. Simple, right? Well, just saying it doesn't mean much, but the pictures will make it easy.
Theory:
The first thing to note is that there are "right rotates" and "left rotates". They're complimentary operations, meaning one undoes the other (the same way if you add a number, a subtraction undoes it. Add 5 to 20 and you get 25. Subtract 5 from that, and you're back to 20).
The first thing to note is that there are "right rotates" and "left rotates". They're complimentary operations, meaning one undoes the other (the same way if you add a number, a subtraction undoes it. Add 5 to 20 and you get 25. Subtract 5 from that, and you're back to 20).
|
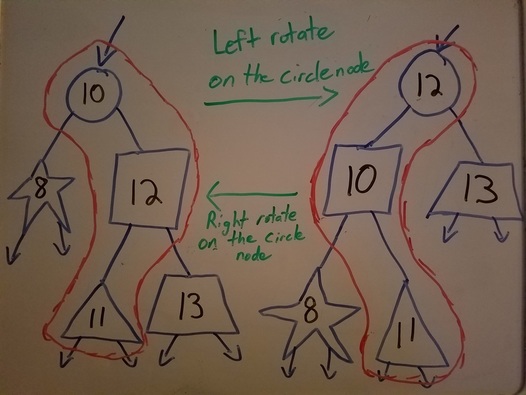
Five nodes are affected by a rotation. The node we rotate does NOT change position, it changes values with another node. The remaining four nodes then shift positions.
If we start with the five nodes on the left (which could be anywhere in a much bigger tree), we can decide to do a left rotate on the 10 node. Since we're calling a left rotate, we look at 10's right child (12) and that right child's left child (11). If we imagine rotating those nodes left (counter-clockwise), then 12 moves up and 10 moves down to be 12's left child. The 11 got disconnected from the 12, but it become's 10's right child. If you look at the right tree and call a right rotate on the 12, we end up in the same position as before. |
Left and right rotates. Pay attention to the shapes of each node and the value inside.
|
The best way to understand this intuitively is to look at before and after of the rotation and imagine rotating the nodes in the red circle, and thinking of where they end up.
In depth code:
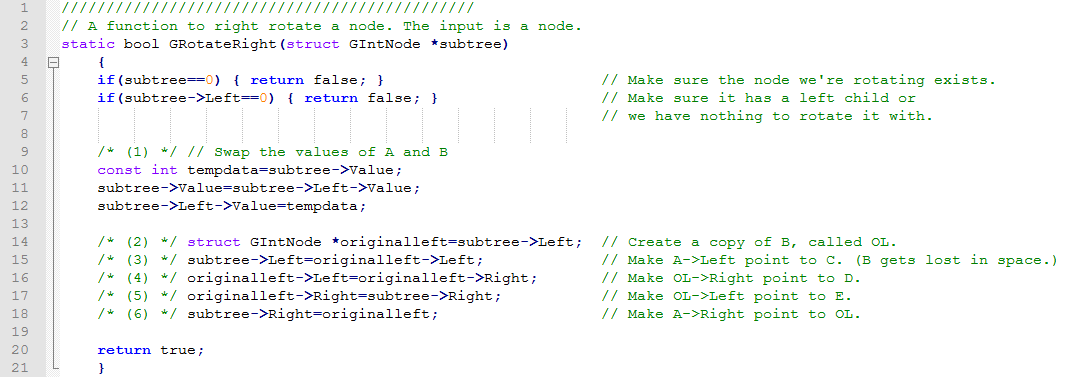
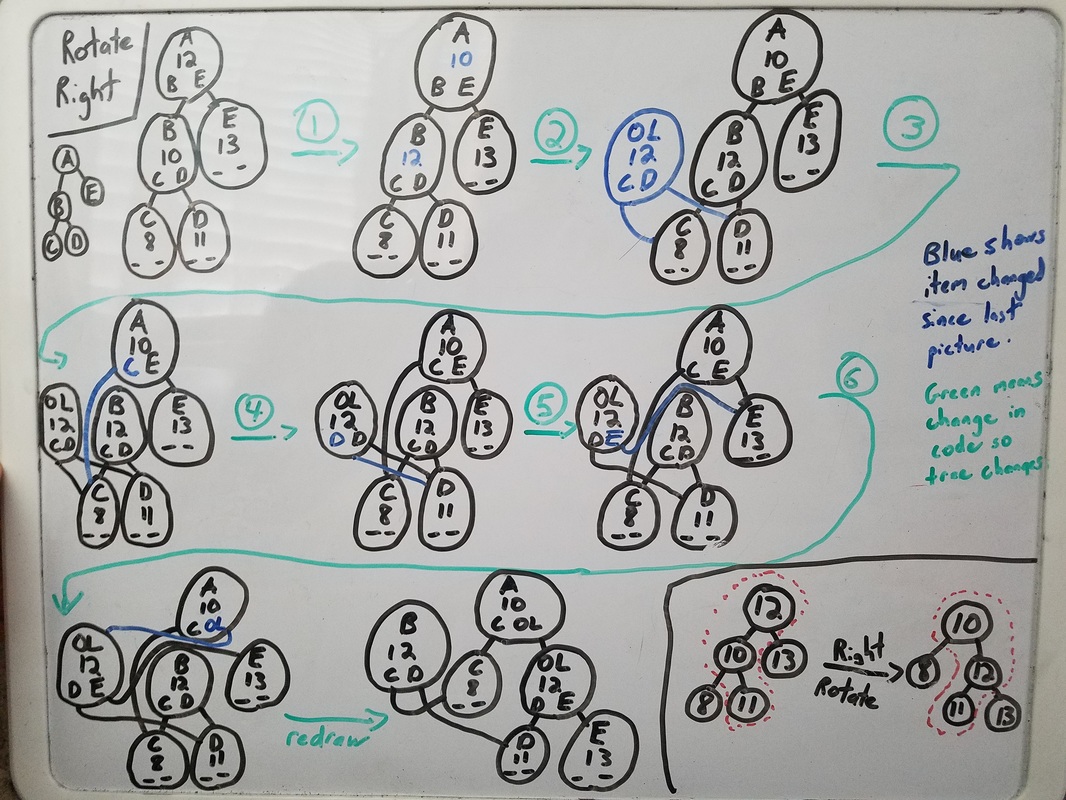
It's all fun and games talking about theories, until we have to write the program. Here's some code for a function that would perform a right rotation on a node. The accompanying picture is a diagram showing exactly what each line of code changes in our tree structure.
It's all fun and games talking about theories, until we have to write the program. Here's some code for a function that would perform a right rotation on a node. The accompanying picture is a diagram showing exactly what each line of code changes in our tree structure.
Written in C. A struct GIntNode has an int Value, a GIntNode Left, and a GIntNode Right.
Showing each step of the code. The top of each node is labeled A, B, C, D, or E for the sake of keeping track of them in the diagram.
The concept of rotating it easy, but the code seems a bit complex. It should seem complex, we're deleting with five nodes, all of which have values and two children to deal with. However, if you follow the diagram for each step you can see what's going on.
A left rotate follows a similar procedure. In the code, change any "Left"s to "Right" and any "Right"s to "Left".
A left rotate follows a similar procedure. In the code, change any "Left"s to "Right" and any "Right"s to "Left".
The DSW Algorithm
So now that we have the fundamentals down, we can actually get to the DSW algorithm part where we take a binary search tree and balance it.
Pro-tip: Unlike AVL trees or self-balancing binary search trees, we only want to call the DSW algorithm once, when our tree is finished and we don't expect any more insertions (or deletions).
Pro-tip: Unlike AVL trees or self-balancing binary search trees, we only want to call the DSW algorithm once, when our tree is finished and we don't expect any more insertions (or deletions).
Logic of DSW
The DSW algorithm is actually very simple. We can define it in two steps.
1. Create a "backbone" by making your binary tree completely straight.
2. Rotate some nodes on the backbone until your tree is balanced.
It's actually as simple as it sounds, but let's flesh this out a bit more.
The DSW algorithm is actually very simple. We can define it in two steps.
1. Create a "backbone" by making your binary tree completely straight.
2. Rotate some nodes on the backbone until your tree is balanced.
It's actually as simple as it sounds, but let's flesh this out a bit more.
|
(1) Creating the Backbone
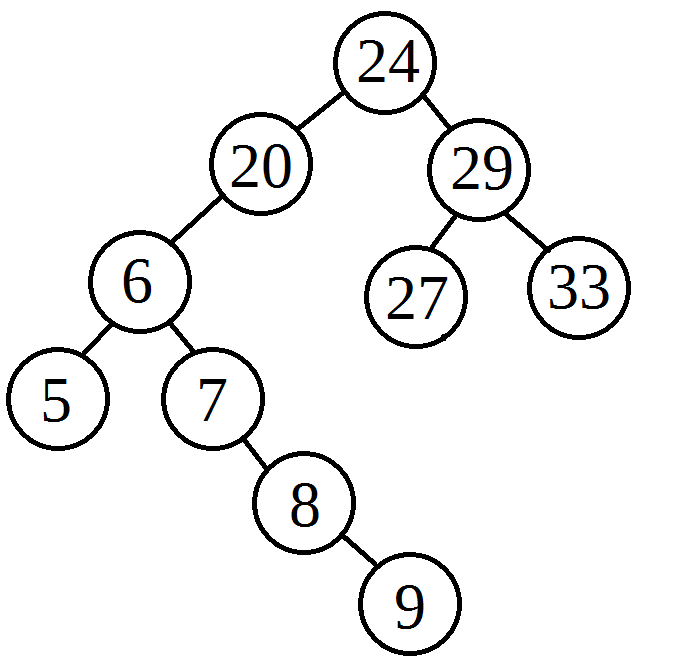
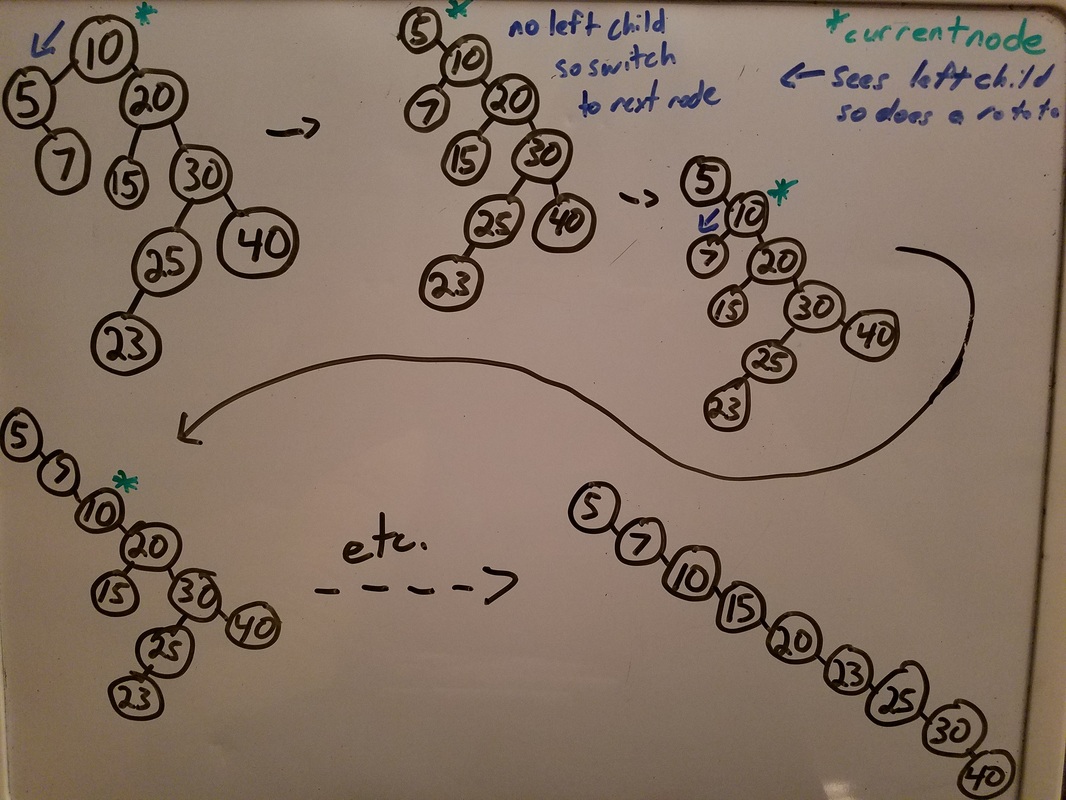
So we want to create a backbone from our tree. This backbone a completely straight (tilted) tree. All nodes in the tree will only have right children. This is surprisingly easy to do. All we need to do is do Right Rotates on every node that has a left child. If we look at the tree given in the picture to the right, we start at the root (10) and see that it has a left child (5). We perform a right rotate on 10 and get the tree that results. We stay at the root (which is now 5) and see that it has no left children, so we move to 5's right child (now 10). We see 10 has a left child (7) so we perform a right rotate on 10, resulting in the tree shown. 7 has no children so we move down to the next right node, which is now 10. We continue this until we get a straight tree. |
A diagram showing how to right rotate all nodes with left children, to create a straight binary tree to serve as our backbone.
|
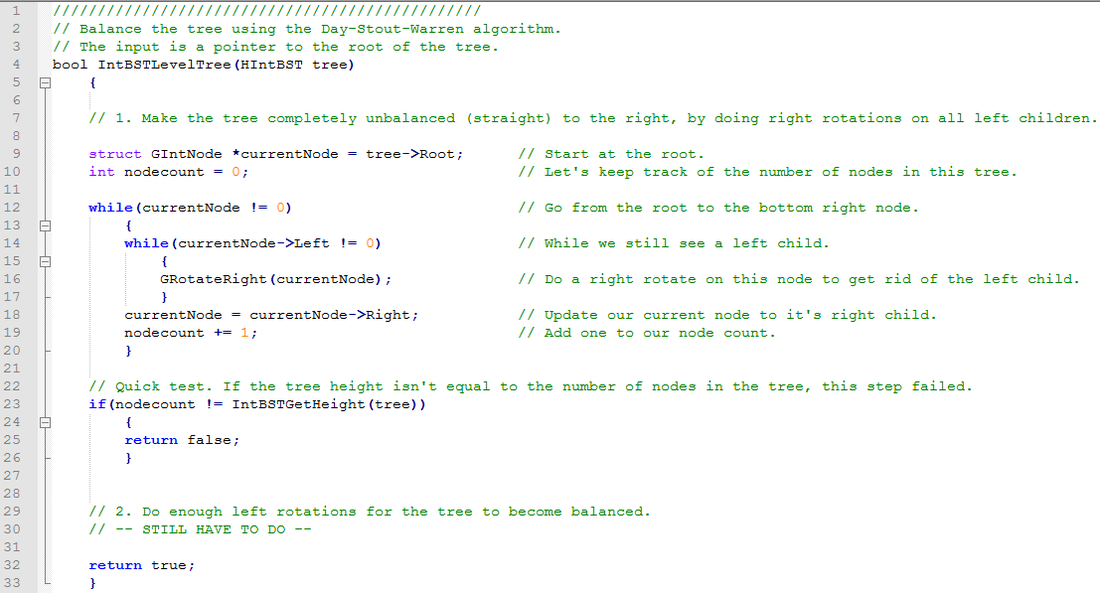
Here's the code corresponding to creating a backbone.
Code for creating the backbone of the DSW algorithm.
|
(2) Balancing the Backbone
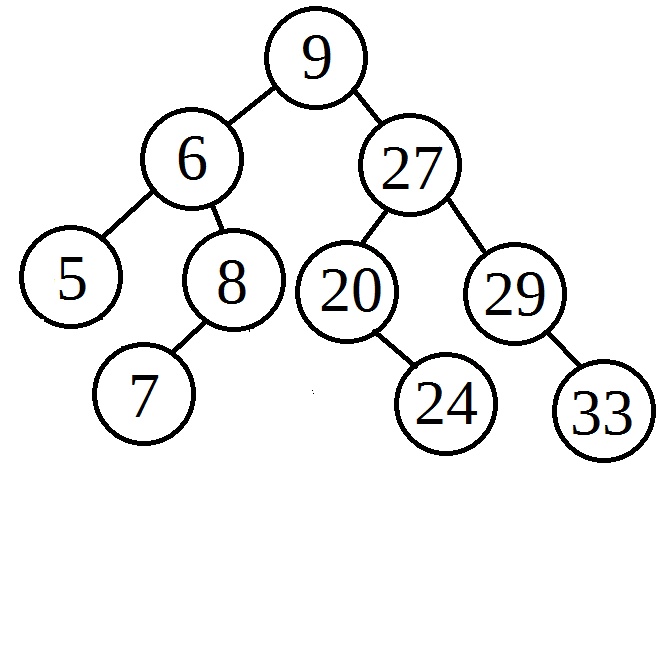
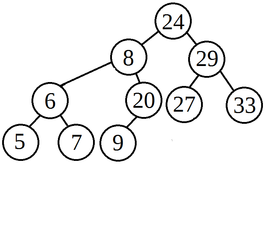
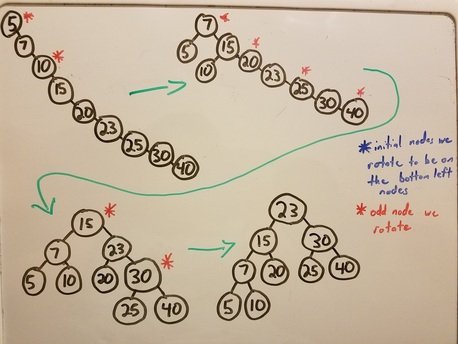
So now we have our backbone, a completely straight tree that is tilted to the right. We have to perform a series of Left Rotates to create a balanced binary tree. The first thing we do is calculate how many nodes we expect on the bottommost level. In the picture to the right, since we have 9 nodes, we expect 2 children on the bottom level. (The top layer will be filled with 1, the second layer will be filled with 2, the third layer will be filled with 4. That leaves 2 for the bottom layer.) We perform Left Rotates on the odd nodes starting from root, going to the bottom right of the backbone. Since we calculated 2, that means the first two odd nodes will be getting left rotated. |
A diagram showing how to left rotate the backbone to get a balanced tree.
|
(Pro-tip: In this initial step, we expect the nodes we rotate to end up on the bottom left of our tree when all is said and done. So we better see 5 and 10 on the bottom left of our tree.)
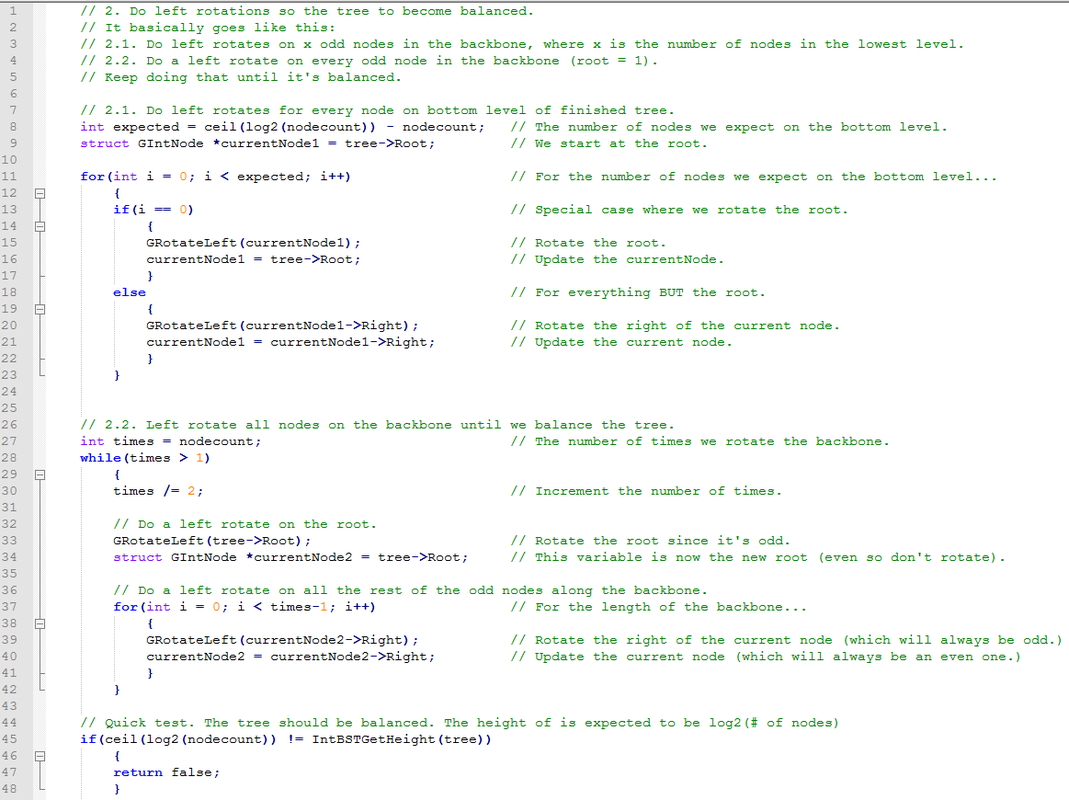
Now that we've done our initial rotation for the bottommost level, we'll begin rotating ALL odd nodes on the backbone. We continue doing this until the tree is balanced. (The number of times we do this will be based on what we expect the height of the tree to be. See the code for an exact formula.)
Now that we've done our initial rotation for the bottommost level, we'll begin rotating ALL odd nodes on the backbone. We continue doing this until the tree is balanced. (The number of times we do this will be based on what we expect the height of the tree to be. See the code for an exact formula.)
Let's look at the code to do this. (This code would go in that "Still have to do" spot in the function above.)
Code for rotating the backbone into a balanced tree using the DSW algorithm.
Source Code:
Here's a zip file containing some C code for implementing a Binary Search Tree. The DSW algorithm is a very small part of the code, however. You'll find it in the IntBST.c file in the 'src' folder.
Alternative to this download, here's the code on Github.
Here's a zip file containing some C code for implementing a Binary Search Tree. The DSW algorithm is a very small part of the code, however. You'll find it in the IntBST.c file in the 'src' folder.
Alternative to this download, here's the code on Github.
| simplebst.zip |
Literature
1. Wikipedia (doesn't help much) - https://en.wikipedia.org/wiki/Day%E2%80%93Stout%E2%80%93Warren_algorithm
2. Stout and Warren's actual research paper (not that helpful) - http://web.eecs.umich.edu/~qstout/pap/CACM86.pdf
3. A research paper explaining the algorithm (helpful) - http://penguin.ewu.edu/~trolfe/DSWpaper/
4. A blog post (very helpful code, actually does "rotations" instead of calling them compressions) - https://xuyuanguo.wordpress.com/2013/02/06/dsw-algorithm-balancing-binary-search-tree/
1. Wikipedia (doesn't help much) - https://en.wikipedia.org/wiki/Day%E2%80%93Stout%E2%80%93Warren_algorithm
2. Stout and Warren's actual research paper (not that helpful) - http://web.eecs.umich.edu/~qstout/pap/CACM86.pdf
3. A research paper explaining the algorithm (helpful) - http://penguin.ewu.edu/~trolfe/DSWpaper/
4. A blog post (very helpful code, actually does "rotations" instead of calling them compressions) - https://xuyuanguo.wordpress.com/2013/02/06/dsw-algorithm-balancing-binary-search-tree/
